你们好,最近小未来发现有诸多的小伙伴们对于方差的计算公式是数学第几章,方差的计算公式这个问题都颇为感兴趣的,今天小活为大家梳理了下,一起往下看看吧。
1、方差是每个数据与其算术平均值的偏差平方和的平均值,通常表示为2。方差的计量单位和量纲在经济学意义上不容易解释,所以在实际统计工作中常用算术平方根——方差标准差来衡量统计数据的差异程度。
 (相关资料图)
(相关资料图)
2、方差和标准差是衡量数据变异程度最重要、最常用的指标。
3、标准差,也叫均方差,一般用表示。方差和标准差的计算也分为简单平均法和加权平均法。此外,对于总体数据和样本数据,公式略有不同。
4、方差是每个数据与平均值之差的平方的平均值。比如这五个数的平均值是3,那么这五个数的方差就是1/5[(1-3)(2-3)(3-3)(4-3)(5-3)]=2。
5、1/n[(x1-x平均值)(x2-x平均值)..(xn-x平均值)]
6、(1)设c为常数,则D(c)=0。
7、(2)若X为随机变量,C为常数,则D (CX)=(C) D (X)。
8、(3)设X和Y是两个随机变量,则
9、D(X+Y)=D(X)+D(Y)+2E{[X-E(X)][Y-E(Y)]}
10、特别是当x和y是两个独立的随机变量,且上式中右边第三项为0(共协方差)时,
11、那么D(X Y)=D(X) D(Y)。这个性质可以推广到有限个独立随机变量之和的情况。
12、(4)d(X)=0的充要条件是X以概率1取常值c,即P{X=c}=1,其中e (x)=c。
13、(5)D(aX bY)=a DX b DY 2 Abe {[X-E(X)][Y-E(Y)]}。
14、设X为随机变量,若e {[x-e (x)]}存在,则e {[x-e (x)]}为X的方差,记为D(X),Var(X)或DX。
15、即d (x)=e {[x-e (x)] 2}称为方差,而 (x)=d (x) 0.5(与x同维)称为标准差(或均方差)。也就是统计学用来衡量一组数据的离散程度。
16、方差描述了随机变量的值与其数学期望值的离散程度。(标准差。方差越大,离散程度越大。否则,否则)
17、如果X的值集中,方差D(X)就小。
18、如果X的值是分散的,方差D(X)更大。
19、所以D(X)是描述X值离散程度的量,是衡量X值离散程度的尺度。
20、根据定义,方差是随机变量x的函数。
21、g(X)=[X-E(X)]^2码头
22、数学期望。即:
23、方差由方差定义,可以得到以下常用的计算公式:
24、d(X)=xisup 2;pi-E(x)sup 2;
25、d(X)=(xisup 2;pi E(X)sup 2;pi-2xipiE(X))
26、=Xi sup 2;piE(X)sup 2;-2E(X)xipi
27、=Xi sup 2;pi E(X)sup 2;-2E(X)超级2;
28、=Xi sup 2;pi-E(x)sup 2;
29、方差实际上是标准差的平方。
30、方差是实际值与期望值之差的平方的期望值,而标准差是方差的算术平方根。在实际计算中,我们用下面的公式计算方差。
31、方差是每个数据与平均值之差的平方的平均值,即s 2=(1/n) [(x1-x_) 2 (x2-x _) 2.(xn-x _) 2],其中x _代表样本的平均值,n代表样本数,xn代表个体。
32、s 2代表方差。
33、当(1/n) [(x1-x _) 2 (x2-x _) 2.(xn-x _) 2]作为样本X的方差的估计,发现其数学期望不是X的方差,而是X的方差的(n-1)/n倍,
34、[1/(n-1)] [(x1-x _) 2 (x2-x _) 2的数学期望.(xn-x _) 2]是X的方差,用它作为X的方差的估计是无偏的,
35、所以我们总是用[1/(n-1)] (xi-x ~) 2来估计x的方差,称之为“样本方差”。
36、方差,通俗点说就是偏离中心的程度!它用来衡量一批数据的波动(即这批数据与平均值的偏差)它被称为这组数据的方差。记录为Ssup2。在样本量相同的情况下,方差越大,数据波动越大。
37、越不稳定。
38、随机变量X。
39、X服从(0—1)分布,则E(X)=p D(X)=p(1-p)
40、X服从泊松分布,即X~ (),则E(X)=,D(X)=
41、X服从均匀分布,即X~U(a,b),则E(X)=(a+b)/2, D(X)=(b-a)^2/12
42、X服从指数分布,即X~e(), E(X)=^(-1),D(X)=^(-2)
43、X服从二项分布,即X~B(n,p),则E(x)=np, D(X)=np(1-p)
44、X 服从正态分布,即X~N(,^2), 则E(x)=, D(X)=^2
45、X 服从标准正态分布,即X~N(0,1), 则E(x)=0, D(X)=1
46、随机变量求方差的通用公式,即D(X)=E(X^2)-[E(X)]^2[
以上就是方差的计算公式这篇文章的一些介绍,希望对大家有所帮助。







 广东省新一轮送教支教活动在西藏林芝市第三幼儿园举行
广东省新一轮送教支教活动在西藏林芝市第三幼儿园举行
 广东医谷:2022年“创客广东”生物医药专题赛圆满落幕
广东医谷:2022年“创客广东”生物医药专题赛圆满落幕
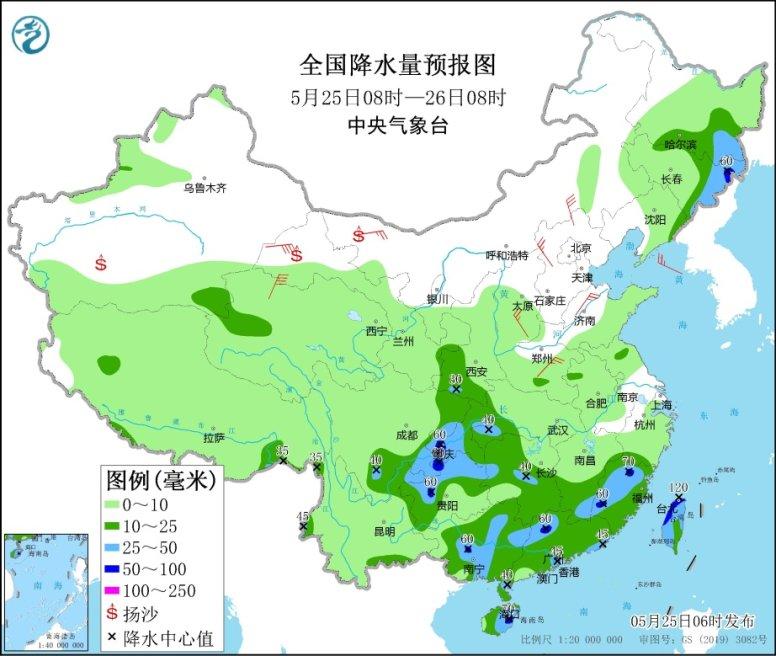
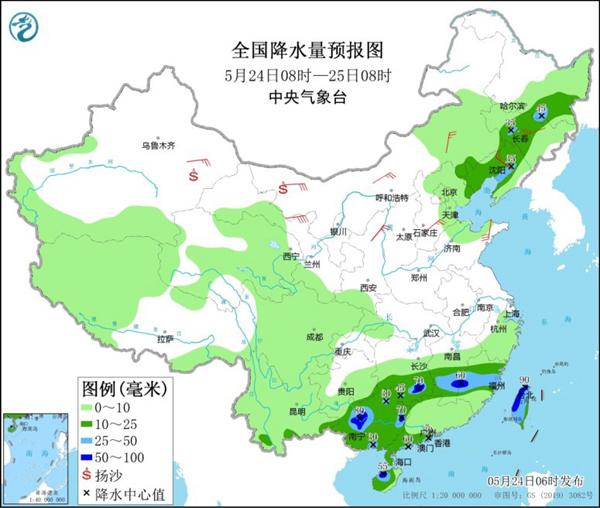
 南方频繁阴雨持续至月底 北方大范围降温
南方频繁阴雨持续至月底 北方大范围降温
 东北黄淮等地有强对流天气 江南华南及贵州等地多降雨
东北黄淮等地有强对流天气 江南华南及贵州等地多降雨
 《只此青绿》被抄袭 舞蹈作品维权难在哪里?
《只此青绿》被抄袭 舞蹈作品维权难在哪里?
Copyright © 2015-2022 北冰洋时尚网版权所有 备案号:沪ICP备2020036824号-3 联系邮箱:562 66 29@qq.com